Researchers at UT Austin Introduce Panda: A Foundation Model for Nonlinear Dynamics Pretrained on 20,000 Chaotic ODE Discovered via Evolutionary Search

Approx systems, such as fluid dynamics or brain activity, are very sensitive to primary conditions, which makes long -term predictions difficult. Even minor errors in modeling these systems can grow quickly, which limits the effectiveness of many scientific learning methods (Sciml). Traditional prediction methods depend on trained models on a specific time series or wide data sets that lack a real dynamic structure. However, the last work has shown the potential of local prediction models to predict chaos more accurately on long time frames by learning the numerical rules governing these systems. The real challenge is to achieve generalization outside the field-the creation of models that can adapt and predict the previously invisible dynamic systems. This requires merge the previous knowledge with the ability to adapt locally. However, the need for task data restricts the current methods and often overlooks the characteristics of the main dynamic system such as Ergodicity, the conjunction of the channel, and the preserved quantities.

Automated learning of dynamic systems (MLDS) uses unique properties of systems such as inductive biases. These include fixed relationships between system variables and fixed statistical measures, such as strange gravity or preserved quantities. MLDS models use these characteristics to build more accurate and generalized models, and sometimes include probable or underlying techniques. While dynamic systems data groups are coordinated and new systems are often created by changing parameters or using symbolic methods, these methods usually do not guarantee various or stable dynamics. Structural stability represents a challenge – the changes that take place may not lead to new behaviors, while those big can cause trivial dynamics. Basic models aim to address this matter by enabling learning to transport and infer zero. However, most of the current models lead relatively to standard or limited chains models in generating a meaningful dynamic diversity. Some progress has been made through techniques such as including spaces or symbolic discovery, but taking richest and more varied samples remains an open challenge.

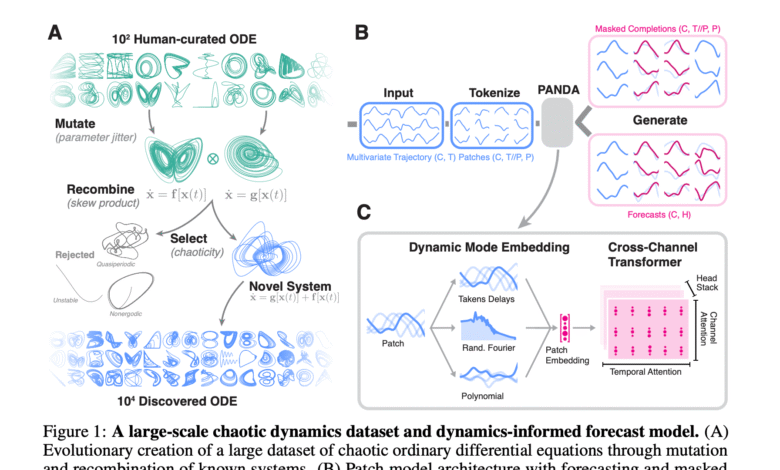
Researchers at the Oden, UT Austin, Panda (Attachment to Non -Sanctuary Dynamics), a pre -trained model on artificial data of 20,000 chaotic systems resulting from algorithm. These systems were created using an evolutionary algorithm based on the well -known chaotic Odes. Despite only training on low-dimensional Odes, PANDA shows a powerful prediction of non-linear systems in the real world-including fluid dynamics and electrical physiology-and is unexpectedly generalized to PDES. The model includes innovations such as persuasive Pretring, the attention of the channel, and the nuclear patch to capture a dynamic structure. The nervous scaling law also appears, with a prediction performance in Panda to the diversity of training systems.

The researchers have created 20,000 new chaotic systems using a genetic algorithm that develops from an appropriate group of 135 well -known chaotic Odes. These systems are mutated and reassembled using the deviation product approach, while really retaining chaotic behaviors through strict tests. Reinforcements such as time delay and Affine transfers expand the data set while maintaining their dynamics. A separate set of 9,300 invisible systems is held for zero test. The model, panda, built on Patchtst and enhances features such as channel attention, attention -to -attention layers and dynamic implications using multi -border features and Furiti, inspired by the theory of Kooopman operator.

Panda shows the powerful prediction capabilities on non-linear dynamic systems, outperforming models such as Chronos-SFT across various standards and prediction prospects. Only trained on 3D systems, it depends on the higher -dimensional systems due to the attention of the channel. Although PDES is not facing during training, Panda also succeeds in experimental data in the real world and chaotic PDES, such as Kuramoto-Sivashinsky and Von Kármán Vortex Street. Architectural meals emphasize the importance of the channel’s attention and dynamics. The model shows nervous scaling with an increase in the diversity of the dynamic system and constitutes interpretable attention patterns, indicating the ringing and the sensitive structure of gravity. This indicates the general circulation of Panda through complex dynamic behaviors.

In conclusion, Panda is a pre -style model for detecting generalized patterns in dynamic systems. Panda has been trained in a large variety of artificial chaos, and has expected a powerful prediction on the inorganical realistic data and even partial differential equations, although it is only trained in low -dimensional Odes. Its performance improves with the diversity of the system, and reveals the nervous scaling law. The model also shows an ungrateful echo arisen in attention patterns. Although focus on low -dimensional dynamics, the approach may extend to high -dimensional systems by taking advantage of separate reactions. Future trends include alternative training strategies to improve the performance of chaotic behavior.

Check the paper. All the credit for this research goes to researchers in this project. Also, do not hesitate to follow us twitter And do not forget to join 95K+ ML Subreddit And subscribe to Our newsletter.

SANA Hassan, consultant coach at Marktechpost and a double -class student in Iit Madras, is excited to apply technology and AI to face challenges in the real world. With great interest in solving practical problems, it brings a new perspective to the intersection of artificial intelligence and real life solutions.