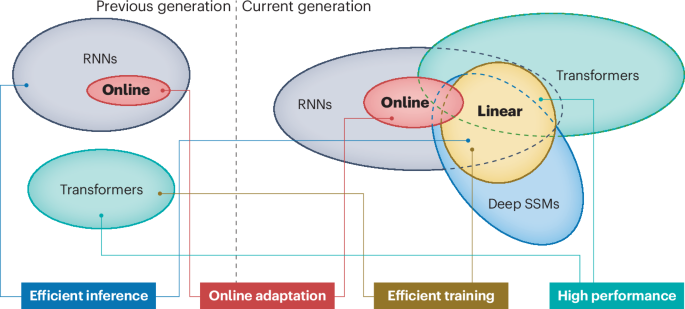
Back to recurrent processing at the crossroad of transformers and state-space models
Brown, T. et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 33, 1877–1901 (2020).
Touvron, H. et al. Llama 2: open foundation and fine-tuned chat models. Preprint at https://doi.org/10.48550/arXiv.2307.09288 (2023).
Gemini team Google. Gemini: a family of highly capable multimodal models. Preprint at https://doi.org/10.48550/arXiv.2312.11805 (2023).
Vaswani, A. et al. Attention is all you need. In Advances in Neural Information Processing Systems Vol. 30 (NuerIPS, 2017).
Yu, Y., Si, X., Hu, C. & Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 31, 1235–1270 (2019).
Google Scholar
Bengio, Y., Mori, R. & Gori, M. Learning the dynamic nature of speech with back-propagation for sequences. Pattern Recognit. Lett. 13, 375–385 (1992).
Google Scholar
Gori, M., Hammer, B., Hitzler, P. & Palm, G. Perspectives and challenges for recurrent neural network training. Log. J. IGPL 18, 617–619 (2010).
Google Scholar
Orvieto, A. et al. Resurrecting recurrent neural networks for long sequences. In International Conference on Machine Learning 26670–26698 (ACM, 2023).
Peng, B. et al. RWKV: reinventing RNNs for the transformer era. In Findings of the Association for Computational Linguistics: EMNLP 2023 (eds Bouamor, H. et al.) 14048–14077 (ACL, 2023).
Voelker, A., Kajić, I. & Eliasmith, C. Legendre memory units: continuous-time representation in recurrent neural networks. In Advances in Neural Information Processing Systems 32 (NeurIPS, 2019).
Gu, A., Dao, T., Ermon, S., Rudra, A. & Ré, C. HiPPO: recurrent memory with optimal polynomial projections. Adv. Neural Inf. Process. Syst. 33, 1474–1487 (2020).
Gu, A., Goel, K. & Re, C. Efficiently modeling long sequences with structured state spaces. In International Conference on Learning Representations (Curran Associates, 2021).
Gu, A. et al. Combining recurrent, convolutional, and continuous-time models with linear state space layers. Adv. Neural Inf. Process. Syst. 34, 572–585 (2021).
Smith, J. T., Warrington, A. & Linderman, S. Simplified state space layers for sequence modeling. In 11th International Conference on Learning Representations (Curran Associates, 2023).
Gu, A. & Dao, T. Mamba: linear-time sequence modeling with selective state spaces. Preprint at https://doi.org/10.48550/arXiv.2312.00752 (2023).
De, S. et al. Griffin: mixing gated linear recurrences with local attention for efficient language models. Preprint at https://doi.org/10.48550/arXiv.2402.19427 (2024).
Marschall, O., Cho, K. & Savin, C. A unified framework of online learning algorithms for training recurrent neural networks. J. Mach. Learn. Res. 21, 5320–5353 (2020).
Google Scholar
Elman, J. L. Finding structure in time. Cogn. Sci. 14, 179–211 (1990).
Google Scholar
Siegelmann, H. T. Neural Networks and Analog Computation: Beyond the Turing Limit (Springer, 2012).
Li, Z., Han, J., E, W. & Li, Q. Approximation and optimization theory for linear continuous-time recurrent neural networks. J. Mach. Learn. Res. 23, 1997–2081 (2022).
Google Scholar
Tallec, C. & Ollivier, Y. Can recurrent neural networks warp time? In International Conference on Learning Representation (Curran Associates, 2018).
Kitagawa, G. A self-organizing state-space model. J. Am. Stat. Assoc. 93, 1203–1215 (1998).
Lipton, Z. C., Berkowitz, J. & Elkan, C. A critical review of recurrent neural networks for sequence learning. Preprint at https://doi.org/10.48550/arXiv.1506.00019 (2015).
Salehinejad, H., Sankar, S., Barfett, J., Colak, E. & Valaee, S. Recent advances in recurrent neural networks. Preprint at https://doi.org/10.48550/arXiv.1801.01078 (2017).
Kidger, P. On neural differential equations. Preprint at https://doi.org/10.48550/arXiv.2202.02435 (2022).
Rumelhart, D. E. et al. Learning Internal Representations by Error Propagation (Institute for Cognitive Science, Univ. California, San Diego 1985).
Werbos, P. J. Backpropagation through time: what it does and how to do it. Proc. IEEE 78, 1550–1560 (1990).
Google Scholar
Pascanu, R., Mikolov, T. & Bengio, Y. On the difficulty of training recurrent neural networks. In International Conference on Machine Learning 1310–1318 (ACM, 2013).
Hochreiter, S. Untersuchungen zu dynamischen neuronalen netzen. Diploma, Technische Univ. München (1991).
Bengio, Y. & Frasconi, P. Credit assignment through time: alternatives to backpropagation. In Advances in Neural Information Processing Systems Vol. 6 (NeurIPS, 1993).
Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
Google Scholar
Cho, K. et al. Learning phrase representations using RNN encoder–decoder for statistical machine translation. In Proc. 2014 Conference on Empirical Methods in Natural Language Processing 1724–1734 (EMNLP, 2014).
Mehta, H., Gupta, A., Cutkosky, A. & Neyshabur, B. Long range language modeling via gated state spaces. In 11th International Conference on Learning Representations (Curran Associates, 2023).
Hua, W., Dai, Z., Liu, H., Le, Q. Transformer quality in linear time. In International Conference on Machine Learning 9099–9117 (ACM, 2022).
Sun, Y. et al. Retentive network: a successor to transformer for large language models. Preprint at https://doi.org/10.48550/arXiv.2307.08621 (2023).
Arjovsky, M., Shah, A. & Bengio, Y. Unitary evolution recurrent neural networks. In International Conference on Machine Learning 1120–1128 (ACM, 2016).
Mhammedi, Z., Hellicar, A., Rahman, A. & Bailey, J. Efficient orthogonal parametrisation of recurrent neural networks using householder reflections. In International Conference on Machine Learning (ACM, 2017).
Kag, A. & Saligrama, V. Training recurrent neural networks via forward propagation through time. In International Conference on Machine Learning 5189–5200 (ACM, 2021).
Sutskever, I., Vinyals, O. & Le, Q. V. Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 27, 3104–3112 (2014).
Karuvally, A., Sejnowski, T. & Siegelmann, H. T. Hidden traveling waves bind working memory variables in recurrent neural networks. In 41st International Conference on Machine Learning (ACM, 2024).
Sieber, J., Alonso, C. A., Didier, A., Zeilinger, M. N. & Orvieto, A. Understanding the differences in foundation models: attention, state space models, and recurrent neural networks. Preprint at https://doi.org/10.48550/arXiv.2405.15731 (2024).
Tay, Y., Dehghani, M., Bahri, D. & Metzler, D. Efficient transformers: a survey. ACM Comput. Surv. 55, 109–110928 (2023).
Google Scholar
Katharopoulos, A., Vyas, A., Pappas, N. & Fleuret, F. Transformers are RNNs: fast autoregressive transformers with linear attention. In International Conference on Machine Learning 5156–5165 (ACM, 2020).
Peng, H. et al. Random feature attention. In Proc. 9th International Conference on Learning Representations (Curran Associates, 2021).
Schlag, I., Irie, K. & Schmidhuber, J. Linear transformers are secretly fast weight programmers. In International Conference on Machine Learning 9355–9366 (ACM, 2021).
Qin, Z. et al. The devil in linear transformer. In Proc. 2022 Conference on Empirical Methods in Natural Language Processing 7025–7041 (EMNLP, 2022).
Schmidhuber, J. Learning to control fast-weight memories: an alternative to dynamic recurrent networks. Neural Comput. 4, 131–139 (1992).
Google Scholar
Qin, Z. et al. Scaling transnormer to 175 billion parameters. Preprint at https://doi.org/10.48550/arXiv.2307.14995 (2023).
Katsch, T. GateLoop: fully data-controlled linear recurrence for sequence modeling. Preprint at https://doi.org/10.48550/arXiv.2311.01927 (2023).
Yang, S., Wang, B., Shen, Y., Panda, R. & Kim, Y. Gated linear attention transformers with hardware-efficient training. In Proc. 41st International Conference on Machine Learning (ACM, 2024).
Dauphin, Y. N., Fan, A., Auli, M. & Grangier, D. Language modeling with gated convolutional networks. In International Conference on Machine Learning 933–941 (ACM, 2017).
Ma, X. et al. MEGA: moving average equipped gated attention. In 11th International Conference on Learning Representations (Curran Associates, 2022).
Zhai, S. et al. An attention free transformer. Preprint at https://doi.org/10.48550/arXiv.2105.14103 (2021).
Peng, B. et al. Eagle and Finch: RWKV with matrix-valued states and dynamic recurrence. Preprint at https://doi.org/10.48550/arXiv.2404.05892 (2024).
Huang, F. et al. Encoding recurrence into transformers. In 11th International Conference on Learning Representations (Curran Associates, 2022).
Dai, Z. et al. Transformer-XL: attentive language models beyond a fixed-length context. In Proc. 57th Annual Meeting of the Association for Computational Linguistics (ACL, 2019).
Bulatov, A., Kuratov, Y. & Burtsev, M. Recurrent memory transformer. Adv. Neural Inf. Process. Syst. 35, 11079–11091 (2022).
Didolkar, A. et al. Temporal latent bottleneck: synthesis of fast and slow processing mechanisms in sequence learning. Adv. Neural Inf. Process. Syst. 35, 10505–10520 (2022).
Munkhdalai, T., Faruqui, M. & Gopal, S. Leave no context behind: efficient infinite context transformers with infini-attention. Preprint at https://doi.org/10.48550/arXiv.2404.07143 (2024).
Gu, A., Goel, K., Gupta, A. & Ré, C. On the parameterization and initialization of diagonal state space models. Adv. Neural Inf. Process. Syst. 35, 35971–35983 (2022).
Gupta, A., Gu, A., Berant, J. Diagonal state spaces are as effective as structured state spaces. In 36th Conference on Neural Information Processing Systems (NeurIPS, 2022).
Massaroli, S. et al. Laughing hyena distillery: extracting compact recurrences from convolutions. In 37th Conference on Neural Information Processing Systems (NeurIPS, 2023).
Martin, E. & Cundy, C. Parallelizing linear recurrent neural nets over sequence length. In International Conference on Learning Representations (Curran Associates, 2018).
Dao, T. et al. Hungry hungry hippos: towards language modeling with state space models. In Proc. 11th International Conference on Learning Representations (Curran Associates, 2023).
Hasani, R. et al. Liquid structural state-space models. In 11th International Conference on Learning Representations (Curran Associates, 2023).
Hasani, R., Lechner, M., Amini, A., Rus, D. & Grosu, R. Liquid time-constant networks. In Proc. AAAI Conference on Artificial Intelligence Vol. 35, 7657–7666 (2021).
Olsson, C. et al. In-context learning and induction heads. Preprint at https://doi.org/10.48550/arXiv.2209.11895 (2022).
Ba, J., Hinton, G. E., Mnih, V., Leibo, J. Z. & Ionescu, C. Using fast weights to attend to the recent past. Adv. Neural Inf. Process. Syst. 29, 4338–4346 (2016).
Jing, L. et al. Gated orthogonal recurrent units: on learning to forget. Neural Comput. 31, 765–783 (2019).
Google Scholar
Orvieto, A., De, S., Gulcehre, C., Pascanu, R. & Smith, S. L. Universality of linear recurrences followed by non-linear projections: finite-width guarantees and benefits of complex eigenvalues. In 41st International Conference on Machine Learning (ACM, 2024).
Tay, Y. et al. Long range arena: a benchmark for efficient transformers. In 9th International Conference on Learning Representations (Curran Associates, 2021).
Poli, M. et al. Hyena hierarchy: towards larger convolutional language models. In International Conference on Machine Learning 28043–28078 (ACM, 2023).
Poli, M. et al. Mechanistic design and scaling of hybrid architectures. In 41st International Conference on Machine Learning (ACM, 2024).
Li, S., Li, W., Cook, C., Zhu, C. & Gao, Y. Independently recurrent neural network (IndRNN): building a longer and deeper RNN. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 5457–5466 (IEEE, 2018).
Beck, M. et al. xLSTM: extended long short-term memory. Adv. Neural Inf. Process. Syst. 37, 107547–107603 (2025).
Qin, Z., Yang, S. & Zhong, Y. Hierarchically gated recurrent neural network for sequence modeling. In Thirty-seventh Conference on Neural Information Processing Systems (NeurIPS, 2023).
Mandic, D. P. & Chambers, J. A. Recurrent Neural Networks for Prediction: Learning Algorithms, Architectures and Stability (John Wiley & Sons, 2001).
Chen, R. T., Rubanova, Y., Bettencourt, J. & Duvenaud, D. K. Neural ordinary differential equations. In Advances in Neural Information Processing Systems Vol. 31 (NeurIPS, 2018).
Rubanova, Y., Chen, R. T. & Duvenaud, D. K. Latent ordinary differential equations for irregularly-sampled time series. In Advances in Neural Information Processing Systems Vol. 32 (NeurIPS, 2019).
Kidger, P., Morrill, J., Foster, J. & Lyons, T. Neural controlled differential equations for irregular time series. Adv. Neural Inf. Process. Syst. 33, 6696–6707 (2020).
Lechner, M. et al. Neural circuit policies enabling auditable autonomy. Nat. Mach. Intell. 2, 642–652 (2020).
Google Scholar
Massaroli, S., Poli, M., Park, J., Yamashita, A. & Asama, H. Dissecting neural odes. Adv. Neural Inf. Process. Syst. 33, 3952–3963 (2020).
Rusch, T. K. & Mishra, S. UnICORNN: a recurrent model for learning very long time dependencies. In International Conference on Machine Learning 9168–9178 (ACM, 2021).
Effenberger, F., Carvalho, P., Dubinin, I. & Singer, W. The functional role of oscillatory dynamics in neocortical circuits: a computational perspective, Proc. Natl. Acad. Sci. USA 122, e2412830122 (2025).
Lanthaler, S., Rusch, T. K. & Mishra, S. Neural oscillators are universal. Adv. Neural Inf. Process. Syst. 36, 46786–46806 (2024).
Irie, K., Gopalakrishnan, A. & Schmidhuber, J. Exploring the promise and limits of real-time recurrent learning. In 12th International Conference on Learning Representations (Curran Associates, 2024).
Feng, L. et al. Attention as an RNN. Preprint at https://doi.org/10.48550/arXiv.2405.13956 (2024).
Dao, T. & Gu, A. Transformers are SSMs: generalized models and efficient algorithms through structured state space duality. In 41st International Conference on Machine Learning (ACM, 2024).
Merrill, W., Petty, J. & Sabharwal, A. The illusion of state in state-space models. In 41st International Conference on Machine Learning 35492–35506 (ACM, 2024).
Hahn, M. Theoretical limitations of self-attention in neural sequence models. Trans. Assoc. Comput. Linguist. 8, 156–171 (2020).
Google Scholar
Peng, B., Narayanan, S. & Papadimitriou, C. On limitations of the transformer architecture. In First Conference on Language Modeling (COLM, 2024).
Zeng, A., Chen, M., Zhang, L. & Xu, Q. Are transformers effective for time series forecasting? In Proc. AAAI Conference on Artificial Intelligence Vol. 37, 11121–11128 (AAAI, 2023).
Jelassi, S., Brandfonbrener, D., Kakade, S. M. & Malach, E. Repeat after me: transformers are better than state space models at copying. In 41st International Conference on Machine Learning (ACM, 2024).
Jiang, A. Q. et al. Mistral 7B. Preprint at https://doi.org/10.48550/arXiv.2310.06825 (2023).
Team, J. et al. Jamba-1.5: hybrid transformer-Mamba models at scale. Preprint at https://doi.org/10.48550/arXiv.2408.12570 (2024).
Glorioso, P. et al. Zamba: a compact 7B SSM hybrid model. Preprint at https://doi.org/10.48550/arXiv.2405.16712 (2024).
Dao, T. FlashAttention-2: faster attention with better parallelism and work partitioning. In 12th International Conference on Learning Representations (Curran Associates, 2024).
Casoni, M. et al. Pitfalls in processing infinite-length sequences with popular approaches for sequential data. In IAPR Workshop on Artificial Neural Networks in Pattern Recognition 37–48 (Springer, 2024).
Zucchet, N., Meier, R., Schug, S., Mujika, A. & Sacramento, J. Online learning of long-range dependencies. Adv. Neural Inf. Process. Syst. 36, 10477–10493 (2023).
Betti, A., Gori, M. & Melacci, S. Learning visual features under motion invariance. Neural Networks 126, 275–299 (2020).
Google Scholar
Tiezzi, M. et al. Stochastic coherence over attention trajectory for continuous learning in video streams. In Proc. 31st International Joint Conference on Artificial Intelligence 3480–3486 (IJCAI, 2022).
Don’t miss more hot News like this! Click here to discover the latest in AI news!
2025-05-15 00:00:00